В 1509 году в книжных лавчонках Венеции появилась небольшая, изящно изданная темнокожая книга. На ее коричневой ворсистой обложке были выдавлены в шахматном порядке матово-золотые слоны. Любители быстро раскупили ее. Почти на каждой странице книги превосходной черной краской были выполнены гравюры, изображавшие разные геометрические фигуры. Слухи упорно приписывали великолепные гравюры руке самого Леонардо да Винчи. На заглавном листе книги автор, некий брат Лука Пачиоли ди Бого, торжественно заявлял о связи идей книги с произведениями великого Платона. Книга называлась «О божественной пропорции» и повествовала об одной из загадок пропорции тел, которую поставила перед человеком природа.

Древнегреческий философ Птолемей (II в. до н. э,) заметил, что высоту человеческой фигуры можно разделить условно на 21 отрезок. Причем большая часть — от пупа до пят — включала 13 отрезков, а меньшая — от пупа до макушки — 8. Измерения тел и статуй, проведенные в дальнейшем Леонардо да Винчи, подтвердили эту закономерность. Выводы настолько поразили его, что он назвал отношение цифр 13:8 золотым отношением, а сам закон — законом золотого сечения. Под этим названием закон и остался в истории.

Немец Цейзинг в своих «Эстетических исследованиях», напечатанных в 1855 году, по сути дела, заново открыл закон золотого сечения, о котором не вспоминали более двухсот лет. Он показал, что этот закон проявляется не только в пропорциях античных статуй и хорошо сложенных людей, но и многих животных, формы которых отличаются грацией и изяществом, и даже насекомых. Наиболее подробно он разработал пропорции Аполлона Бельведерского.

Цейзинг дал строгое определение золотому сечению и показал, как можно его получить. Нужно взять отрезок любой длины и разделить его на две неравные части так, чтобы меньшая из них относилась к большей, как эта большая ко всему отрезку. Но после того как цифры возможных длин отрезков были получены, Цейзинг с удивлением обнаружил, что все они составляют так называемый ряд Фибоначчи: 0,1,1,2,3,5,8,13,21,34,55,89,144…

Каждый легко может продолжить этот ряд до бесконечности, так как члены его обладают любопытным свойством — любой из них равен сумме двух предыдущих: 0+1 = 1; 1 + 1=2; 1+2 = 3; 2 + 3=5; 3 + 5 = 8 и т. д.

Теперь, имея ряд, можно было легко уточнить численное выражение закона, Для этого каждый последующий член ряда нужно просто делить на предыдущий: 2:1=2; 3:2 = 1,5; 5:3=1,666; 8:5=1,6; 13:8 = = 1,625; 21 : 13=1,615…

Если такие отношения подсчитывать дальше и дальше, то мы, в конце концов, придем к бесконечной десятичной дроби 1,618…, которая и есть наиболее точный коэффициент золотого сечения. Эту бесконечную дробь заменяют обычно буквой «Ф».

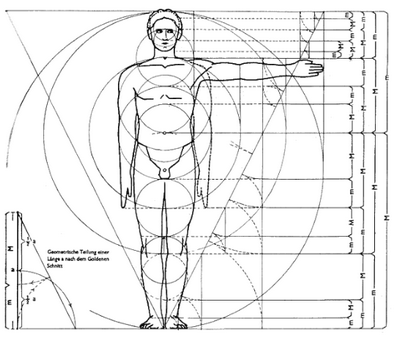
Цейзинг попытался приложить шкалу золотого сечения не только к пропорциям живых существ, но к архитектуре, археологии. Он увидел «свой» закон в некоторых эллинских храмах, в частности в Парфеноне. Парфенон и закон золотого сечения! Высшее проявление прекрасного в архитектуре оценивается рядом Фибоначчи! Цейзинг буквально потрясен. Радостный и надеющийся, что его имя станет рядом с именами великих первооткрывателей законов природы — Ньютона, Гаусса, Галилея, он уверенно называет свою новую книгу: «Золотое деление как основной морфологический закон в природе и искусстве».

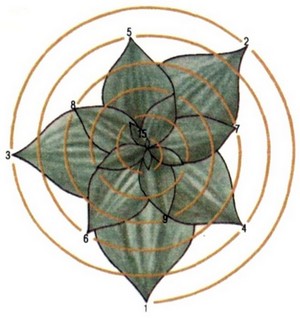
Рамки действия закона золотого сечения с середины XIX века начали стремительно расширяться. Трудно назвать какого-нибудь большого математика, в трудах которого не осталось бы заметок по этому закону. Например, русский математик Ю. В. Вульф пришел к золотому сечению, изучая расположение листьев на стебле растения. Многие искусствоведы выявили, как они считали, существование закона золотого сечения в музыкальных произведениях, длительность отдельных частей которых находится в том же соотношении. Историки искусства оповестили мир, что в основу расчетов пропорций большинства сооружений положено правило золотого сечения. В этот спор внесли свою лепту даже… повара. Оказалось, что отношение между большой и малой осями большинства птичьих яиц тоже подчиняется великому закону.

Так закон золотого сечения незримо внедрился в наше сознание, вошел во многие стороны жизни. Как это ни удивительно, но даже формат большинства картин, книг, листов бумаги, открыток — не что иное, как прямоугольник с отношением сторон, совпадающим с золотым или близким к нему. В конце XIX века вряд ли можно было встретить хотя бы одну статью или книгу по эстетике, в которой не были бы соседями понятие прекрасного и закон золотого сечения. Впрочем, этот великий закон «Божественной пропорции» или «золотого сечения» незримо присутствует на всех прекрасных вещах, когда либо созданных в прошлом, и тех, которые когда-либо будут созданы в будущем.

Автор: Повийленко Рюрик.

P. S. Духи вещают: Интересно, что закон золотого сечения действует в самых разных областях нашей жизни. Даже в такой как СЕО. Вот скажем надо вам монетизировать свой сайт, и даже нашлась хорошая партнерка с олатой за показы, что нужно сделать, чтоб сами показы были эффективными? Правильно, чтоб показы были эффективными, их необходимо размещать на сайте за принципом золотого сечения.